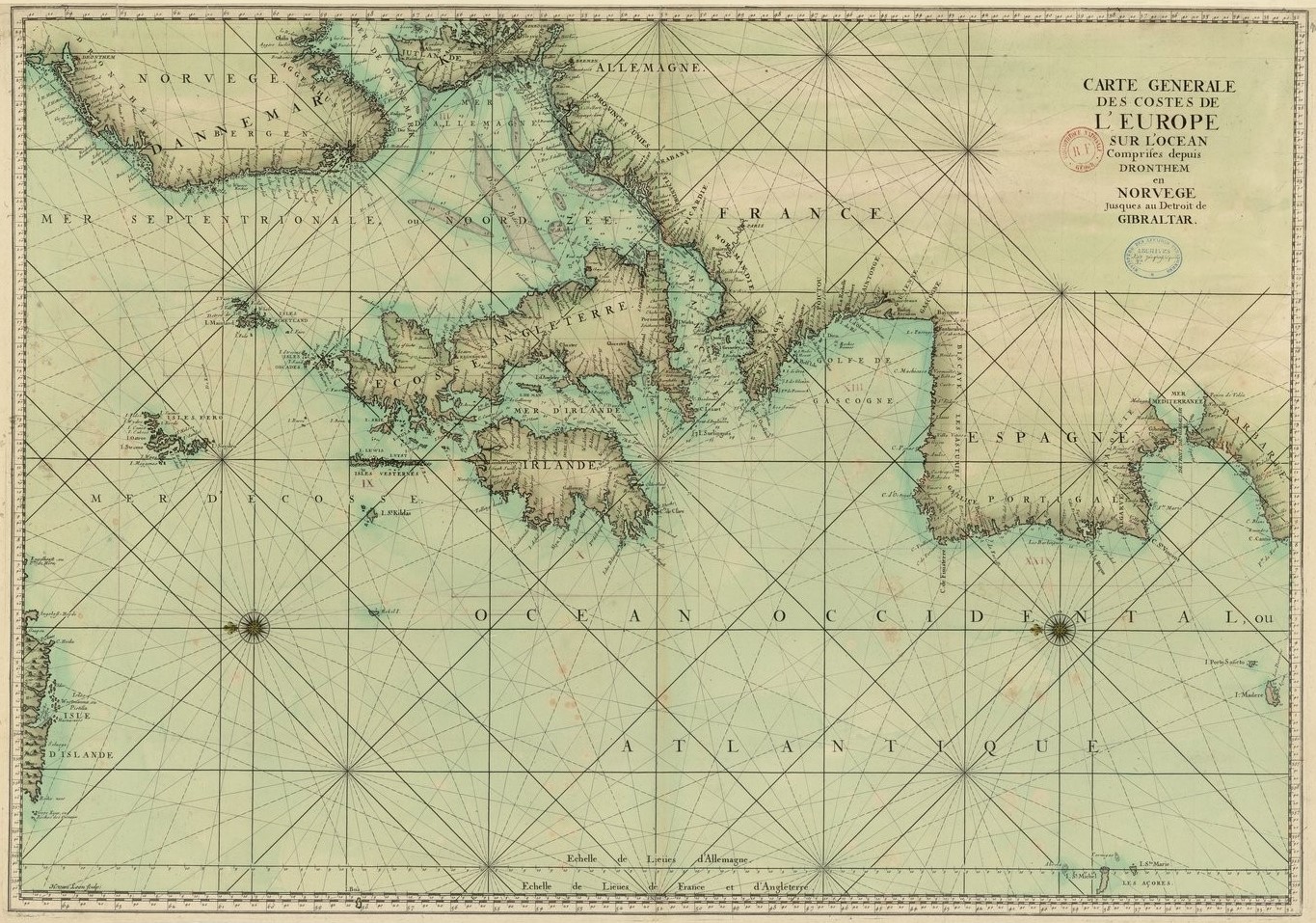
Carte générale des costes de l’Europe sur l’Océan … depuis Drontheim … jusques au détroit de Gibraltar
Joseph Sauveur (1653-1716), Cartographe ; Charles Pene, Auteur adapté ; Herman Van Loon, (16..-17..? ; graveur). Graveur. Éditeur : à Paris
Bassin d’Arcasson
Appartient à : Collection d’Anville ; 00183 B
Cette carte est extraite du « Neptune françois » (ou « Recueil des cartes marines levées et gravées par ordre du Roy. Premier volume contenant les costes de l’Europe sur l’Océan depuis Dronthem en Norvege jusques au détroit de Gilbraltar, avec la mer Baltique ») de Charles Pène, dont la première édition sortit des presses de l’Imprimerie royale en 1693. Les huit cartes des côtes de Bretagne sont l’ouvrage de M. de La Voye, ingénieur de la Marine, qui les a levées pendant les années 1675, 1676 et suivantes, MM. Sauveur et Pène les ont copiées pour les insérer dans le Neptune François.
Le Neptune François est une entreprise officielle à laquelle collaborent, à l’initiative du ministre Colbert, les mathématiciens et astronomes de l’Académie des sciences et les ingénieurs hydrographes de la Marine.
Sa première édition sort des presses de l’imprimerie royale en 1693. Le privilège a été accordé le 27 décembre 1691 à Charles Pène, ingénieur géographe chargé des cartes et plans du roi. L’ouvrage est annoncé dans le « Journal des Sçavans » du 11 janvier 1694 ; on y apprend qu’il est en vente chez Claude Gournai, sur le quai de l’Horloge du Palais. Il offre 29 cartes des côtes d’Europe, de la Norvège à Gibraltar.
Un deuxième volume est annoncé pour la Méditerranée, mais il ne parut jamais.
Des détails sur la réalisation du « Neptune » sont contenus dans son édition de 1753. Ses deux principaux maîtres d’œuvre sont Sauveur, maître de mathématiques des enfants royaux et membre de l’Académie des sciences, et Chazelles, ingénieur de la Marine et membre de la même Académie.
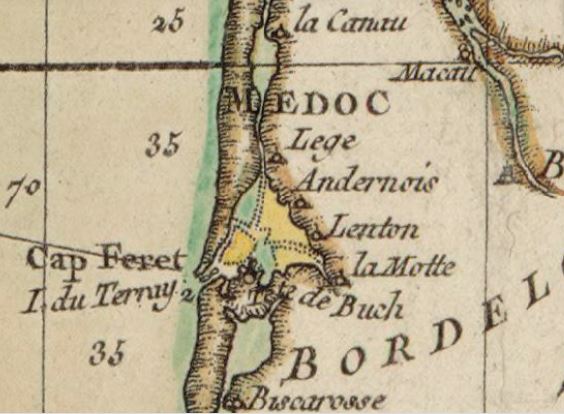
1763 – Neptune françois Rizzi-Zannoni – Cap Feret, I. du Terray, Tete de Buch, la Motte, Lenton, Andernois, Lege
Le petit Neptune françois ou Carte des côtes maritimes du Royaume avec une partie de celles d’Angleterre
dans laquelle on voit les ports ou havres, les bayes, les rades, les sondes, les bancs de sable, les rochers, écueils, caps, etc. Giovanni-Antonio Rizzi-Zannoni, (1736-1814). Cartographe à Paris)
Cap Feret, I. du Terray, Tete de Buch, la Motte, Lenton, Andernois, Lege
D’origine italienne, installée plus de vingt ans à Paris, Giovanni Antonio Bartolomeo Rizzi Zannoni est considéré comme l’un des principaux cartographes et géographes de son temps. Naît le 2 septembre 1736 à Padoue et mort le 20 mai 1814 à Naples, il fait ses études à l’université de Padoue (1749-1751) puis voyage en Turquie et en Russie. En 1753, il commence sa carrière de géographe en Pologne au service du roi Auguste III. En 1756, il s’installe en Suède et au Danemark où il chargé de mesures géodésiques dans les comtés d’Oldenburg et de Delmenhorst (aujourd’hui en Allemagne). L’année suivante, il passe au service de la Prusse et participe à la guerre de Sept Ans. Il est alors fait prisonnier le 7 décembre 1757 à la bataille de Rossbach et envoyé à Paris. Il y reste plus de vingt ans. Il dresse alors une carte du royaume de Naples et est nommé Premier hydrographe du Dépôt des cartes et plans de la Marine (1772-1775).
De retour à Padoue en 1776, il se lance dans une cartographie géodésique et astronomique de l’Italie qui restera inachevée puis dans son travail le plus célèbre, l’Atlas géographique du royaume de Naples qu’il achève en 1812.
https://gallica.bnf.fr/ark:/12148/btv1b8593267k/f1.item.r=Neptune%20Fran%C3%A7ois.zoom
& dito 1778
https://gallica.bnf.fr/ark:/12148/btv1b8439161q.r=Rizzi-Zannoni?rk=386268;0
https://fr.wikipedia.org/wiki/Giovanni_Rizzi-Zannoni
Joseph Sauveur 1653 – 1716
On connaît sa biographie par l’Éloge que fit de lui Bernard le Bovier de Fontenelle (1657-1757), à l’Académie royale des sciences en 1716.
Joseph Sauveur est né le 24 mars 1653 à La Flèche de Renée des Hayes et de Louis Sauveur, notaire.
Il est muet jusqu’à l’âge de sept ans; l’organe de la voix ne se développa ensuite chez lui qu’avec beaucoup de lenteur, et il ne l’eut jamais bien libre.
Il fait ses études au collège de jésuites de La Flèche, mais, avant qu’il y arrive, son goût pour la mécanique s’est déjà manifesté. Dès l’enfance, il est machiniste, construit de petits moulins, fait des siphons avec des chalumeaux de paille, des jets d’eau, etc.
« Il est, dit Fontenelle, l’ingénieur des autres enfants, comme Cyrus devint le roi de ceux avec qui il vivait. »
Cette passion exclusive pour les objets de précision et de calcul le rend un fort médiocre écolier de rhétorique : les chefs-d’œuvre des orateurs et des poètes de l’Antiquité n’ont aucun attrait pour lui ; un mauvais traité d’arithmétique, celui de Peletier du Mans, lui tombe par hasard sous la main : il en est charmé et l’apprend seul
Désirant dès lors se livrer aux sciences et aux arts, Sauveur se rend à pied à Paris, en 1670. Se trouvant à Lyon, il veut entendre la fameuse horloge de la cathédrale Saint Jean, construite, en 1598, par le Suisse Nicolas Lippius. On sait que cette horloge offre plusieurs phénomènes mécaniques à l’admiration de la multitude pour qui la mesure très précise du temps est de peu d’importance ; Sauveur, par le simple examen extérieur de ces phénomènes, devine le mécanisme intérieur.
Un de ses oncles, chanoine et grand chantre de Tournus, lui a promis de subvenir, par une petite pension, à son entretien à Paris, mais sous la condition qu’il y ferait les études nécessaires pour entrer dans l’état ecclésiastique. Le Traité d’Euclide, dont il apprend les six premiers livres en un mois, et sans maître, et les leçons du physicien Rohault, attirent bien plus fortement son attention que ses cahiers de théologie. Il essaie d’abord de changer la carrière ecclésiastique contre celle de la médecine, d’anatomie et de botanique ; grâce à un lecteur du dauphin, M. de Cordemoi, il est présenté à l’évêque de Condom, futur évêque de Meaux, qui lui déconseille de continuer la médecine, au profit des mathématiques. Son oncle lui ayant retiré sa pension, Sauveur, pour subsister à Paris, enseigne les mathématiques, et s’adonne, sans réserve, à ces sciences et à leurs applications.
À cette époque, le peu de personnes qui s’occupent de géométrie sont isolées de la société, et semblent former une classe à part. Sauveur, par une disposition qui lui est propre, peut-être aussi mu par le premier exemple que Rohault a donné dans l’enseignement de la philosophie naturelle, est moins sauvage que ses confrères. Selon de Fontenelle, il devient alors le « Géomètre » à la mode, et obtient des élèves de la haute aristocratie. Sa sociabilité lui vaut quelques connaissances agréables et utiles : citons les services que lui rend Mme de La Sablière, celle qui, pendant plus de vingt ans, logea chez elle La Fontaine.
Sauveur n’a que vingt-trois ans, lorsqu’un illustre élève, le prince Eugène, le prend pour son maître de géométrie. Un étranger, de très haute naissance, voulut apprendre de lui la Géométrie de Descartes ; Sauveur ne connaissait pas encore le Traité de ce grand philosophe : en huit jours et autant de nuits d’étude, il se met en état de le professer.
Il se livre, pendant l’hiver, à ce travail opiniâtre, bien plus par goût que par spéculation, ne s’embarrassant nullement si son feu est allumé ou éteint, et se trouvant, à l’apparition du jour, transi de froid sans s’en être aperçu.
La chaire de mathématiques de Ramus étant devenue vacante au Collège royal, Sauveur aurait pu concourir avec beaucoup de chances de succès pour l’obtenir ; mais une condition imposée à chaque concurrent est de prononcer, de mémoire, un discours de sa composition ; et Sauveur, ne voulant pas ou n’osant pas s’y soumettre, se retire du concours.
Il s’occupe, de 1678 à 1680, de la résolution de divers problèmes relatifs à la théorie des probabilités applicable aux jeux de hasard, à la mode dans la bonne société (Bassette, Quinquenove, Hocca, Lansquenet).
En 1680, il est nommé maître de mathématiques des pages de Mme la Dauphine, et donne des cours d’anatomie à la cour à Fontainebleau.
En 1681, il collabore avec Mariotte, sur les questions d’hydraulique à Chantilly (des tables pour les dépenses des jets d’eau).
Le grand prince Louis de Condé prend beaucoup de goût et d’affection pour lui. Il le fait souvent venir de Paris à Chantilly, et l’honore de ses lettres. C’est pendant le temps de ces voyages, et vraisemblablement par suite de l’impulsion que lui donnent ses entretiens avec un guerrier illustre, qu’il entreprend la composition d’un « Traité de fortifications », qui lui vaut l’amitié de Vauban. Voulant joindre la pratique à la théorie, il alla au siège de Mons, en 1691. « Il y montait tous les jours la tranchée. Il exposait sa vie seulement pour ne négliger aucune instruction ; et l’amour de la science était devenu chez lui un courage guerrier. Le siège fini, il visita toutes les places de Flandre. Il apprit le détail des évolutions militaires, les campements, les marches d’armées, enfin tout ce qui appartient à l’art de la guerre, où l’intelligence a pris un rang au-dessus de la valeur même. » Vauban aurait recommandé Sauveur pour le remplacer à son grade de maréchal.
Revenu à Paris, il s’occupe de diverses recherches et travaux ayant pour objet l’application des mathématiques : méthodes abrégées pour les grands calculs, table pour la dépense des jets-d’eau, cartes des côtes de France, réduites à la même échelle, et composant le premier volume de l’ancien Neptune français ; concordances des poids et mesures de différents pays ; méthode pour le jaugeage des tonneaux ; problèmes sur les carrés magiques, etc.
Il entend la théorie du calcul différentiel et intégral, nouvelle de son temps ; et il s’en sert même, mais il n’en fait pas beaucoup de cas. Il désigne par l’épithète d’infinitaires les partisans de cette théorie, que le XVIIIe siècle a bien vengée de ses dédains !
Il obtient, en 1686, au Collège royal (collège de France), la chaire de mathématiques, que la condition de la harangue à réciter lui a fait manquer huit ou dix ans auparavant. Il n’écrit pas ses leçons, les improvise au tableau, et achète, à la fin de l’année, une des copies manuscrites qu’on en a faites sous sa dictée. Le plaisir de professer, surtout quand il rencontre des auditeurs attentifs et intelligents, lui font souvent oublier l’heure, et il aurait prolongé indéfiniment ses leçons, si un domestique n’était chargé de l’avertir lorsque leur durée excédait certaines limites.
Il a le titre de lecteur et professeur de mathématiques du roi (1692).
En 1696, il est nommé membre de l’Académie des Sciences. Ses droits à un pareil honneur sont incontestables ; cependant rien de ce qu’il a fait jusqu’alors ne jetterait, à l’époque actuelle, du lustre sur sa mémoire, si, à dater de sa réception à l’Académie et pendant les vingt dernières années de sa vie, il ne s’était occupé, avec autant de constance que de succès, à créer une nouvelle branche des sciences physico-mathématiques, qu’on désigne par le nom d’acoustique musicale.
La théorie du son envisagée sous le point de vue musical, est encore, à la fin du XVIIe siècle, à-peu-près au même point où les Anciens nous l’ont laissée. La légende des marteaux de forgerons, pesés par Pythagore, atteste l’ignorance de ceux qui l’ont imaginée et de ceux qui l’ont répétée. Cependant c’est à ce philosophe qu’on doit les premières expressions, en nombre, des rapports des longueurs des cordes, qui, à identité de matière et à égalité de grosseur et de tension, font sonner ces cordes les principaux intervalles. On sait d’ailleurs que, dans son école, les explications des phénomènes du monde, tant intellectuel que physique, se liaient à des notions généralisées de musique, d’harmonie, à de prétendues puissances des nombres ; et des hommes beaucoup plus récents, à qui nous devons de bien grandes découvertes, n’ont pas été tout-à-fait exempts de ces préjugés. Cependant les découvertes de Pythagore, malgré les développements qu’on leur a donnés après lui, et les diverses applications qu’on en a faites, ne peuvent pas être regardées comme constituant une branche des sciences physico-mathématiques. Le domaine de ces sciences est accru d’une importante conquête à la fin du XVIIe siècle, et au commencement du XVIIIe siècle, et c’est à Sauveur qu’on doit cette conquête.
On n’apprendra pas, sans quelque étonnement, que Sauveur, à qui nous devons pourtant l’acoustique musicale, a la voix et l’oreille fausses ; il est obligé, dans ses expériences, de se faire seconder par des musiciens très exercés à apprécier les intervalles et les accords. Les premiers détails publiés sur ses recherches d’acoustique se trouvent dans le volume de l’Académie des sciences de 1700 (Histoire, page 131 et suiv.) ; mais ses premiers travaux, sur cette matière, datent de 1696 : une partie des leçons qu’il donne au Collège royal, en 1697, a pour objet la Musique spéculative, dont il dicte un Traité. Il se refuse aux instances qu’on lui fait pour l’engager à publier ce Traité, par diverses raisons qu’il expose dans son Mémoire sur le système général des intervalles des sons, etc. (volume de l’Académie de 1701, page 299 et suiv.), l’une desquelles est relative à l’attention qu’il a donnée, postérieurement, aux phénomènes des sons harmoniques. Nous allons donner une idée de la découverte fondamentale de Sauveur, celle qui fait de l’acoustique une branche de la physique. On sait, avant lui, que lorsque, caeteris paribus, deux cordes ont leurs longueurs dans le rapport de 1 à 2, ou dans celui de 2 à 3, ou dans celui de 3 à 4, etc., la plus courte sonne respectivement l’octave, la quinte, la quarte, etc., du son rendu par la plus longue ; il est assez aisé d’en conclure que les rapports entre les nombres de vibrations de ces cordes, pendant un même temps, une seconde, par exemple, sont les rapports inverses de leurs longueurs. Avec de pareilles notions, on peut, dans tous les temps et dans tous les lieux, disposer, sans le secours de l’oreille, un système de cordes sonores, de manière qu’elles rendent des sons ayant entre eux des intervalles déterminés ; ainsi sachant que la lyre en Trépied de Pythagore sonne les modes dorien, lydien et phrygien, et consultant, d’ailleurs, les détails qu’Athénée nous a transmis sur cet instrument, on a les moyens d’obtenir une série de sons dans les mêmes rapports entre eux que ceux de cette lyre antique. Mais s’il s’agit de réunir à la condition de l’égalité des rapports, celle de l’identité des sons, la solution du problème serait impossible, les anciens ne nous ayant laissé aucun moyen de retrouver l’unisson d’une des cordes de leur système musical. Peut-être avaient-ils, comme nous, de ces instruments métalliques, connus sous le nom de diapasons, qui gardent et transmettent un son fixe : mais ces instruments sont altérables et périssables, et le problème de la réhabilitation de l’unisson doit pouvoir se résoudre sans égard à la conservation d’aucun monument matériel ; c’est ce que Sauveur fait, le premier, en assignant le nombre absolu ou effectif de pulsations ou de vibrations que fait, dans un temps donné, et dans des circonstances déterminées, soit un tuyau d’orgue, soit une corde sonore. Ainsi il trouve que la corde sonnant l’ut double octave au-dessous de l’ut de la clef, à l’unisson du tuyau d’orgue, à bouche, de huit pieds ouvert, vibre cent vingt-deux fois dans une seconde ; et comme sa solution fournit des règles certaines pour mettre une corde sonore quelconque en état de vibrer un nombre de fois assigné pendant un temps donné (pourvu qu’elle ait la force de supporter la tension convenable), on saura, dans tous les temps et dans tous les lieux reproduire l’unisson, soit de notre ut, soit de toute autre corde de notre système musical, par des opérations absolument indépendantes de l’usage d’aucun conservateur matériel d’unisson.
On lui doit aussi, entre autres, en 1692, « Explication des échelles pour les calculs de marine, pour servir d’introduction aux cartes marines gravées par ordre du Roy ».
Joseph Sauveur a été marié deux fois. Les deux fils issus du premier mariage sont ingénieurs aux armées. De son second mariage, un fils sera abbé et conseiller au parlement de Paris, amateur de calcul. De sa fille, Fontenelle ne dit rien.
https://gallica.bnf.fr/ark:/12148/btv1b53052916z
http://recherche-archives.vendee.fr/ark:/22574/vta3977195de64dd5e2
https://catalogue.bnf.fr/ark:/12148/cb40618442p
https://www.musicologie.org/Biographies/s/sauveur_joseph.html
https://gallica.bnf.fr/ark:/12148/bpt6k166184v/f2.item
http://www.cosmovisions.com/Sauveur.htm
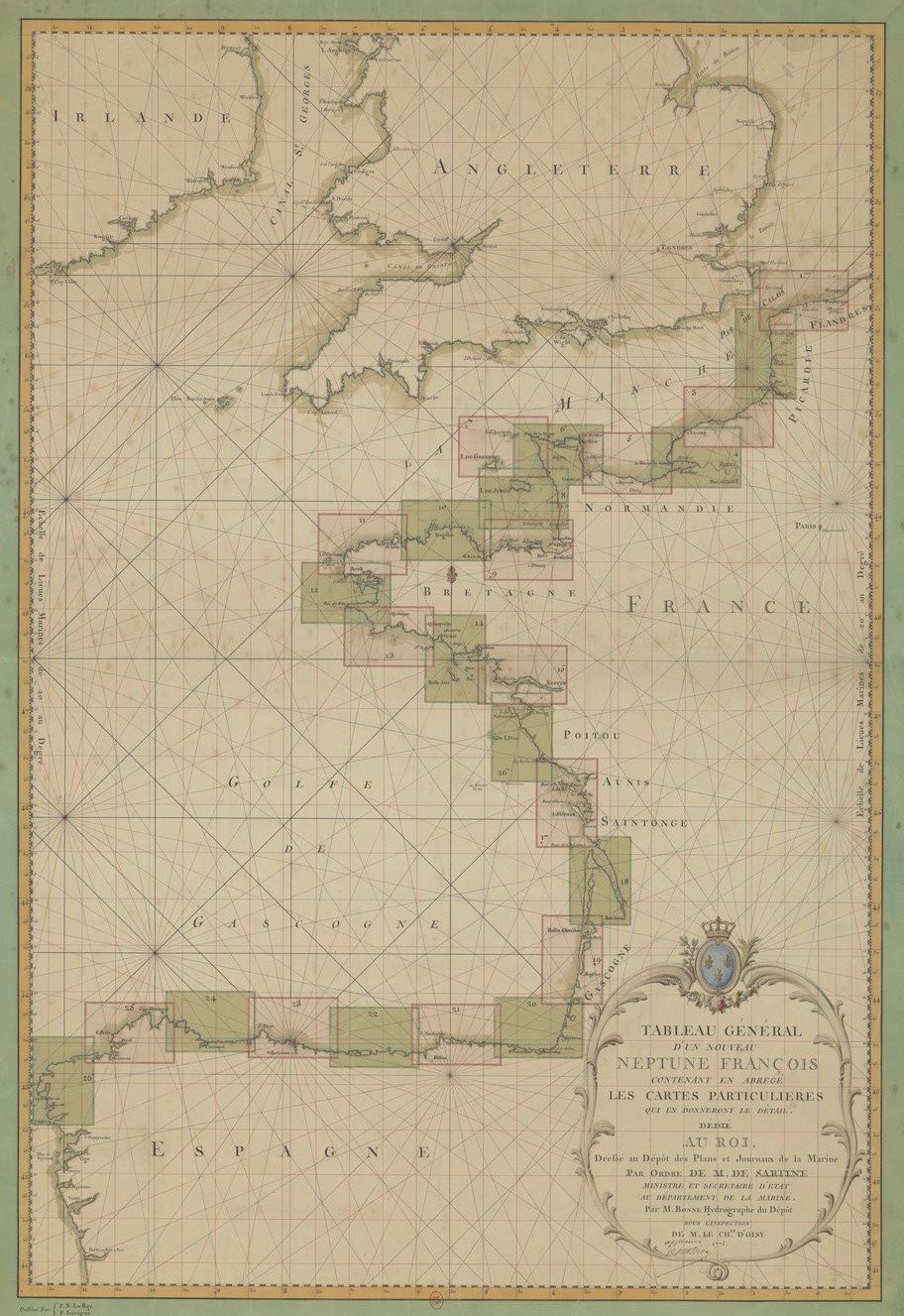
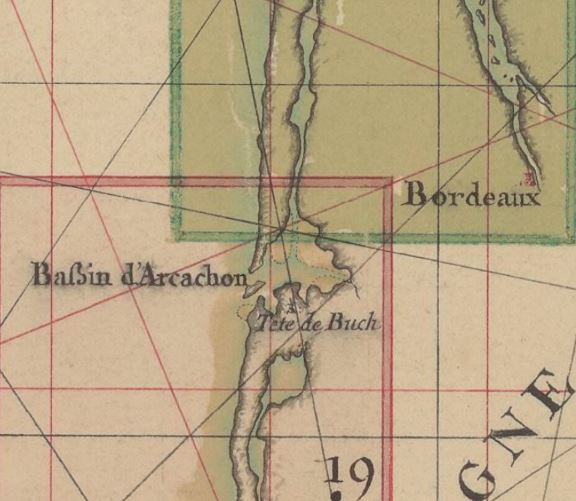
1775 – Tableau général d’un nouveau Neptune François – Bassin d’Arcachon, Tete de Buch
Tableau général d’un nouveau Neptune François…,
Rigobert Bonne, Cartographe
Bassin d’Arcachon, Tete de Buch
Dès 1753, Jacques-Nicolas Bellin, auteur du replâtrage du Neptune françois semble néanmoins conscient qu’il faudra à terme faire du neuf avec autre chose que de l’ancien. Trois ans plus tard – à l’occasion de ses études de cabinet sur le golfe de Gascogne – Fleurieu (il n’a alors que dix-huit ans) réfléchit probablement à cette nécessité. Mais le plan ne prend forme qu’après la nomination dc Gabriel-Joseph d’Oisy à la tête du Dépôt, en 1773. Le projet de nouveau Neptune françois est la conséquence logique des critiques imputables à la mauvaise réimpression de l’original.
En 1775, le chevalier d’Oisy engage Rigobert Bonne pour qu’il réfléchisse à une carte générale des côtes occidentales de France sur une seule et même échelle, et dont les trente-deux feuilles se chevaucheraient afin de permettre le passage de l’une à l’autre sans coupure dommageable pour les navigateurs. Afin de préparer ce travail, Bonne calcule la latitude et la longitude des points secondaires en utilisant une formule algébrique à partir de leur distance à la méridienne et à sa perpendiculaire. Avant les levés, il fait aussi dresser un canevas à très grand point, sur lequel figurent « les sondes, les bancs de sable, les rochez, des cartes qu’on irai lever afin qu’on n’ait plus qu’à y marquer les changemens que les opérations indiqueroient ». Curieuse méthode de travail que celle consistant à porter sur la minute, avant les mesures sur le terrain, ce qu’on s’attend à y trouver. Comme si les cartes n’avaient besoin que de légères retouches…
https://gallica.bnf.fr/ark:/12148/btv1b53011196n.r=%22Neptune%20Fran%C3%A7ois%22?rk=42918;4
À la mer comme au ciel : Beautemps-Beaupré & la naissance de l’hydrographie moderne (1700-1850), Olivier Chapuis, 1999.
Voir
Modèles de topographie et signes conventionnels : adoptés par les ingénieurs hydrographes de la Marine, et employés sur les cartes et plans du Nouveau Neptune français / écrit par Besançon ; gravé par Blondeau
https://gallica.bnf.fr/ark:/12148/btv1b53147916n.r=%22nouveau%20neptune%22?rk=42918;4
Rigobert Bonne (1727-1794) est un géographe, ingénieur hydrographe et cartographe français, maitre de mathématique.
Né dans les Ardennes à Raucourt le 6 octobre 1727. Il apprend les mathématiques sans maître et il est ingénieur à dix-huit ans. Il sert en cette qualité dans la guerre de Flandre, où il se trouve au siège de Berg-op-Zoom en 1747.
Il s’applique à la physique, aux mathématiques, à la géographie et il est, durant quinze ans, un des maîtres les plus recherchés de Paris. Il succède en 1775 à Giovanni Rizzi-Zannoni comme cartographe du Roi de France au Service Hydrographique de la Marine (le Dépôt des cartes et plans de la Marine est créé sur ordre du Roi Louis XV en 1720).
Une attaque de paralysie lui survient en 1775 ; il lui reste une infirmité pour le reste de sa vie.
Vers 1780, il définit précisément la projection qui portera alors son nom : la Projection de Bonne.
Il a entre autres produit des cartes pour les ouvrages de l’abbé Raynal et pour l’Encyclopédie méthodique de Nicolas Desmarest.
Il est victime, vers le milieu de l’année 1795, d’une hydropisie à laquelle il succomb le 2 novembre. Son fils Charles-Marie Rigobert dit le chevalier Bonne (25 juin 1771 – 23 novembre 1839), poursuit son œuvre.